The P-Delta Effect and P-Delta Analysis: Understanding Structural Stability
In the world of structural engineering, ensuring the stability and reliability of buildings is of paramount importance. One crucial aspect of structural analysis is the consideration of the P-Delta effect and the utilization of P-Delta analysis. In this blog post, we will delve into the fundamentals of the P-Delta effect, explain the significance of P-Delta analysis, and explore its implications for structural stability. So, let’s get started and unravel the mysteries of the P-Delta effect!
What is the P-Delta Effect?
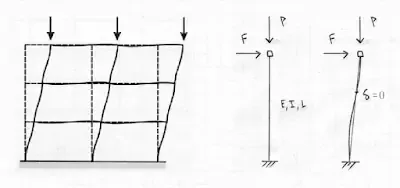
The P-Delta effect refers to the second-order effects that occur in structures subjected to lateral loads. When a structure experiences deformations due to lateral loads, it undergoes a change in geometry, resulting in internal forces that can significantly affect its stability. The P-Delta effect takes into account the interaction between the applied loads and the resulting deformations, which can have a substantial impact on the structural response.
Understanding P-Delta Analysis
P-Delta analysis is a sophisticated method used to incorporate the P-Delta effect into structural analysis. It accounts for the interaction between the axial forces (P) and the lateral displacements (Delta) to accurately predict the structural response under lateral loads. By considering the geometric nonlinearity caused by lateral deflections, P-Delta analysis provides a more realistic representation of the structure’s behavior compared to traditional linear analysis methods.
Significance of P-Delta Analysis
P-Delta analysis is essential for assessing the stability of structures subjected to lateral loads, such as wind or seismic forces. Neglecting the P-Delta effect can lead to underestimating the internal forces and deformations, potentially compromising the safety and integrity of the structure. Incorporating P-Delta analysis ensures a more accurate prediction of the structural behavior, enabling engineers to design safer and more reliable structures.
Factors Influencing the P-Delta Effect
Several factors influence the magnitude and significance of the P-Delta effect. These factors include:
- Structural Configuration: The geometry and stiffness of the structure play a crucial role in determining the extent of the P-Delta effect. Irregular or slender structures are more susceptible to significant P-Delta effects.
- Loading Conditions: The magnitude, direction, and distribution of the applied loads influence the P-Delta effect. As the lateral loads increase, the P-Delta effect becomes more pronounced.
- Material Properties: The stiffness and strength characteristics of the materials used in the structure affect the P-Delta effect. More flexible materials are more susceptible to larger P-Delta effects.
Benefits of Incorporating P-Delta Analysis
- Improved Accuracy: By considering the P-Delta effect, engineers can obtain more accurate predictions of the structural response, ensuring a higher level of safety and reliability.
- Optimal Design: P-Delta analysis enables engineers to optimize the design by identifying critical elements prone to instability and implementing suitable measures to enhance structural performance.
- Code Compliance: Many design codes and standards require the consideration of the P-Delta effect, and incorporating P-Delta analysis ensures compliance with these regulations.
P-Delta analysis parameters in Etabs
Initial P-Delta analysis may be specified in ETABS via Define>P-Delta Options and using either of the following two methods:
1. Non-iterative Based on Mass, in which load is automatically computed from the mass at each level. This is an approximate method which does not require an iterative solution, providing for faster computation. P-Delta is considered by treating the structure as a simplified stick model, a process which is most effective with a single rigid diaphragm at each level. Local buckling is not captured as effectively.
The benefit of this non-iterative method is that P-Delta may be considered in load cases which do not specify gravity load. When gravity load is specified, we generally recommend the Iterative Based on Load Cases method.
2. Iterative Based on Load Cases, in which load is computed from a specified combination of static load cases, then known as the P-Delta load combination. This is an iterative method which considers P-Delta on an element-by-element basis. Local buckling is captured more effectively. An example application may be when load includes the dead load case and a fraction of a live load case.
When the iterative method is selected, two additional options become available :
- Convergence Tolerance (Relative), Iteration is used to make sure that equilibrium is achieved at each step of the analysis. Use this parameter to set the relative convergence tolerance that is used to compare the magnitude of force error with the magnitude of the force acting on the structure. Using a smaller value ensures better equilibrium, although the default value is usually adequate.
- P-Delta Load Combination, in which users may specify the single load combination for the initial P-Delta analysis.
For example, suppose that a building code requires the following load combinations:
(1) 1.4 dead load
(2) 1.2 dead load + 1.6 live load
(3) 1.2 dead load + 0.5 live load + 1.3 wind load
(4) 1.2 dead load + 0.5 live load – 1.3 wind load
(5) 0.9 dead load + 1.3 wind load
(6) 0.9 dead load – 1.3 wind load
A P-Delta load combination of 1.2 DL + 0.5 LL is typically conservative when considering P-Delta effect due to the overall sway of a structure.
Combinations (3) and (4) will accurately capture this effect, while (5) and (6) should be conservative. Combinations (1) and (2) have no lateral load,
therefore P-Delta effect should not be of concern. Please notice this is a non-linear static case and should be performed only after the model runs without any numerical issues for simple linear cases and results of basic variables such as deformations are within realistic or expected values.
P- effect
ETABS may account for P- effect, which is associated with local deformation relative to the chord between member ends. We do not recommend implementing this method because it will significantly increase computational time without providing the benefit of useful information. Instead, P- may be captured through either of the following methods:
- Apply design factors, which ETABS post-processing assumes to be done. These factors are therefore included in design, when applicable.
- Divide members into segments (at least two per column), then run each load case separately with a different P-Delta load combination for each.